LE CARRÉ MAGIQUE d'ALBRECHT DÜRER
Nous verrons dans un article spécialement consacré au Feng-Shui, une technique chinoise, les implications des carrés magiques.
Mais je ne peux m'empêcher de vous transmettre immédiatement cette exception découverte par Albrecht DÜRER en 1514 !
LE GENIAL ALBRECHT DÜRER (1471 - 1528)
ET SON CARRÉ MAGIQUE !
 Autoportrait qu'il fit à l'âge de 28 ans
Autoportrait qu'il fit à l'âge de 28 ans
Petit fils d’un orfèvre Hongrois immigré à Nuremberg, le père d’Albrecht devient orfèvre à son tour et part pour faire son apprentissage ; il découvre VITRUVE et inclut le canon de la « Divine Proportion » dans ses œuvres gravées (cf. l'article spécialement consacré à la « Divine Proportion » sous le titre « NOMBRE D’OR & HARMONIE »...)
Selon la tradition familiale, son jeune fils Albrecht est lui aussi destiné au métier d'orfèvre.
À 13 ans, il devient donc apprenti chez son père pendant trois ans et apprend à se servir du burin et de la pointe. Voyant les dons de son fils pour le dessin, son père lui donne la permission d'entrer dans l'atelier d'un peintre.
C'est ainsi qu'en 1486, il devient l'apprenti de Michael WOLGEMUT, avec qui il apprend à manier la plume et le pinceau, à copier et dessiner d'après nature, à réaliser des paysages à la gouache et à l'aquarelle et également à peindre à l'huile. Il se familiarise également avec la technique de la gravure sur bois. Il y reste trois ans et se familiarise avec l’ésotérisme.
Il s’intéresse ainsi aux « Carrés Magiques » qui sont, dans les ésotérismes juif et islamique, associés à des connaissances secrètes qui furent transmises, pendant et avant l'époque de DÜRER par des confréries d'ésotérisme chrétien qui maintenaient des relations suivies avec les initiés à l'ésotérisme islamique.
En ordonnant les nombres de 1 à 2, 3, 4, 9, 25, etc... (ou tout autre nombre carré supérieur à 4), une grille carrée peut être remplie de façon telle que la somme sur chaque ligne horizontale, verticale ou diagonale ait la même valeur.
Les carrés magiques utilisés dans l'hermétisme sont d'ordre « n », c'est-à-dire qu'ils ont « n » lignes et « n » colonnes, correspondant aux nombres entiers allant de 1 à n2. La somme de tous les nombres d'un tel carré magique de taille « n » a pour valeur :
1 + 2 + ... + n² = n² (n² + 1)
2
tandis que la valeur de ce carré, c'est-à-dire le même nombre que l'on retrouve en sommant les lignes, les colonnes, ou les deux diagonales vaut, puisqu'il y a « n » lignes et « n » colonnes, la quantité précédente divisée par « n », c'est-à-dire :
1 + 2 + ... + n² = n (n² + 1)
n 2
Les différentes tailles « n » sont mises en correspondance avec les « cieux » dans les représentations traditionnelles, ainsi :
Le carré d'ordre 3, (n=3) et de valeur 15, correspond au « ciel de Saturne ». Je me permets de m'y attarder quelques minutes pour donner le ton... il est encore appelé le carré magique « Lo Shu »
Une très ancienne légende rapporte qu’à l’origine il a été découvert en Chine, sur les bords du « fleuve Lo » (le « fleuve Jaune ») par l’empereur FU-XI (ou FO-HI) lui-même, vers 2400 avant J.C., qui, en observant une tortue d'eau qui marchait sur la berge du fleuve, fut frappé par le motif des écailles de sa carapace… dans lequel il distinguait un damier de neuf cases. Celle du centre contenait 5 taches, et les autres 1, 2, 3, 4, 6, 7, 8 et 9 taches.
En vérité, comme on a pu le découvrir au siècle dernier, les chiffres dit arabes (parce que ce sont les arabes qui les ont véhiculé, exception faite du zéro ainsi que le carré magique (appelé encore carré de Saturne) qui ne sont pas d’origine chinoise mais proviennent des Indes.
Ce même carré à 9 cases, ornait la chevalière du roi Salomon…
Nota bene : Comme nous l'avons vu plus haut, les chiffres de 1 à 9 sont disposés de telle manière qu'en les additionnant verticalement, horizontalement ou en diagonale. Le nombre « 15 » s'impose toujours. La somme de tous ses nombres vaut 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45, et sa valeur est 15.
Il y a d'autres carrés magiques dont les sommes demeurent constantes, mais celui-là est exceptionnel parce qu'il n’utilise que les seuls chiffres de 1 à 9 et il est unique, à savoir qu'il ne permets qu'une seule disposition de ses chiffres alors que plusieurs disposition peuvent être trouvées pour les carrés d'ordre supérieur à 3 !
Le Carré magique d'ordre 3 a inspiré par la suite ce même empereur chinois FU-XI et ses successeurs, la création de « trigrammes » symbolisant l'évolution constante des choses et la célèbre théorie du YIN CH'I et du YANG CH'I combinant ainsi deux éléments binaires des trigrammes, le YIN et le YANG.
Le carré d'ordre 4, (n = 4) et de valeur 34, est attribué à Albrecht DÜRER, tel celui que l'on trouve dans la « Melencolia » (une gravure de ce même DÜRER qu’il a faite en 1514 – cf. plus loin). Il est associé au « Ciel de Jupiter ».
La somme de tous ses nombres vaut 136.
On peut proposer plusieurs dispositions des nombres du carré d'ordre 4 (et des carrés d'ordre n > 4) mais celui de DÜRER est un type bien particulier de carré magique: la somme dans l'un de ses quatre quadrants, ainsi que la somme des nombres du carré du milieu, valent également 34, la valeur du carré.
On l'a appelé carré magique « Gnomon ». car tous ses chiffres sont répartis autour d'une colonne centrale assimilable à un « Gnomon » ou pieu central (cf. mon article sur l'Harmonie du Nombre d’Or).
Vers la fin du XVe siècle Luca PACIOLI a été le premier à publier des exemples de carrés magiques mais il est possible que DÜRER ait eu connaissance du manuscrit De Philosophia Occulta que Cornelius AGRIPPA avait déjà rédigé vers 1510.
L'arrangement particulier qu'il a choisi, comporte, au milieu de la dernière ligne, les nombres 15 et 14 qui correspondent à la date de confection de la gravure, 1514. De plus, étant lié avec Jupiter, par son caractère « jovial » ce carré devrait être une influence bénéfique contre la mélancolie. Les propriétés numérologiques de cet élément de la gravure peuvent donner l'occasion à de nombreuses interprétations.
Ici, ce sont les nombres 3 et 4 qui sont significatifs : ils apparaissent de façon symétrique dans la Tétraktys pythagoricienne: 1 + 2 + 3 + 4 = 10 = 3 + 4 + 3. Ce carré magique est relié à une certaine interprétation cyclique du dénaire (i.e. qui contient le nombre 10 en base 10). Dans le cas de la gravure, il est lié à une interprétation de nature apocalyptique.
Dans ce carré magique, si on se réfère aux carrés intérieurs, en parcourant le sens des aiguilles d'une montre, on trouve la suite consécutive des nombres 14, 15, 16, 17, 18, 19, 20, avec un dédoublement pour la valeur 17. la somme de tous ses nombres vaut 136.
Gravure « Melencolia » d'Albrecht DURER.
En haut à droite de la gravure « Melencolia », sur la stèle, juste en dessous de la cloche, se trouve ce carré magique créé par DÜRER. Il apparait grossi sur la photo que j'ai extrait ci-dessous à gauche pour le faire apparaître encore plus clairement, j'en ai fait une épure plus claire à droite :
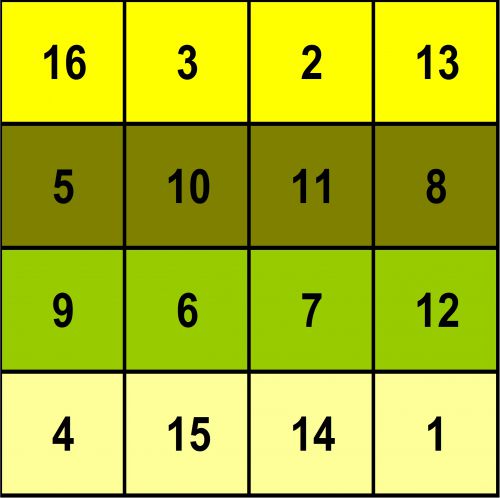
Et qu’est-ce qui est magique ? C’est le nombre 34 qui est la somme des différents champs du carré, je m’explique :
la somme de chaque rangée est égale à 34 !... La somme de chaque colonne est égale à 34 !... Mais la somme des 4 coins, à savoir 4 + 16 + 13 + 1, est encore égale à 34 !
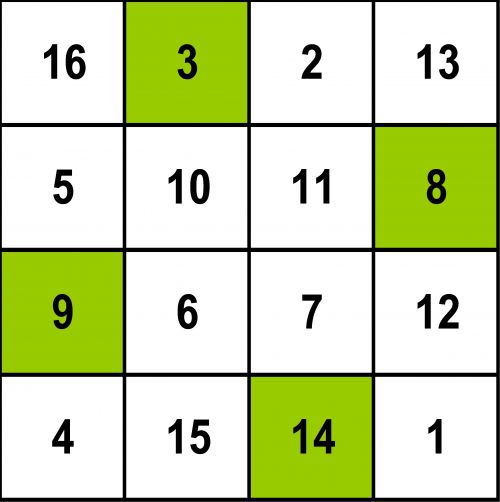
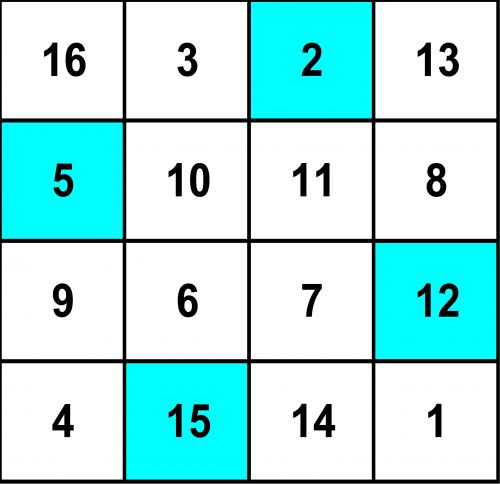
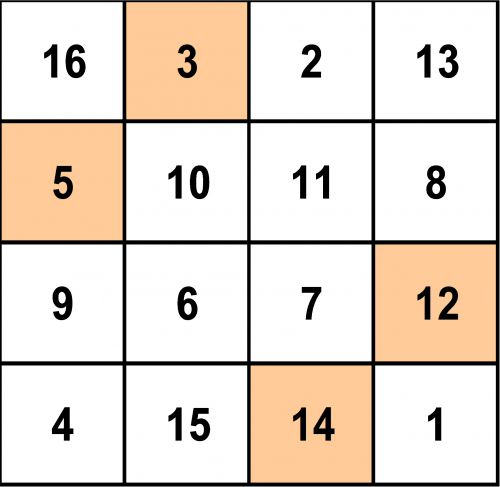
Déplacez les champs dans le sens des aiguilles d'une montre (dextrogyre) et la somme 3 + 8 + 14 + 9 = 34 ! Et déplacez les champs encore une fois et la somme 5 + 2 + 12 + 15 est toujours = 34!
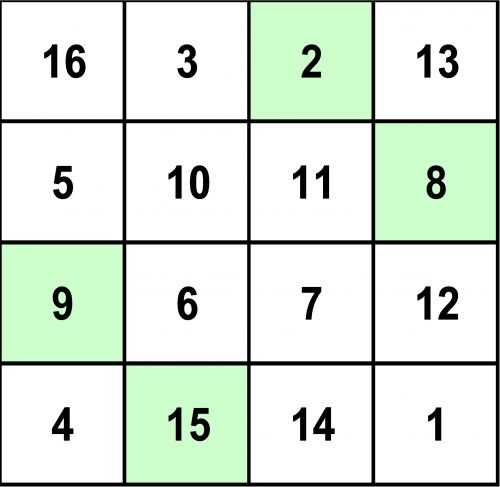
La somme des champs au milieu 10 + 11 + 6 + 7 = 34 !
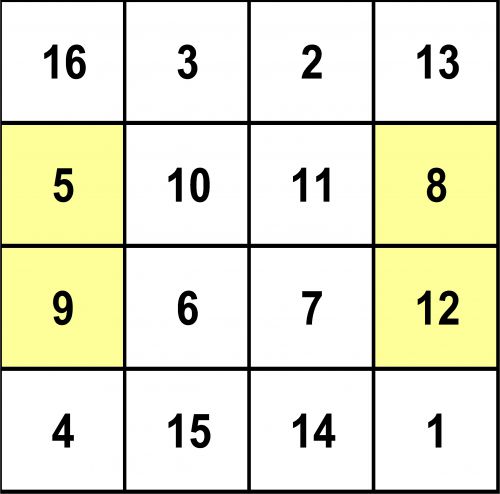
Tout comme sur les cotés 5 + 9 + 8 + 12 = 34 !
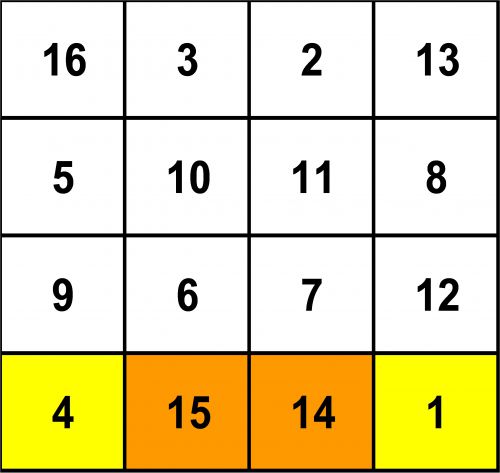
Tout comme en haut et en bas où 3 + 2 + 15 + 14 = 34 !
C’est toujours vrai pour les diagonales... 4 + 6 + 11 + 13 = 34 et 16 + 10 + 7 + 1 = 34 !
Et ainsi de suite, en tournant dextrogyre... 5 + 3 + 12 + 14 = 34 ! Mais encore 2 + 8 + 15 + 9 = 34 !
Bref, DÜRER a créé ce carré en 1514. Et pur hasard cette fois, si le C de « Carré » est la 3ème lettre de l'alphabet, le D de « DÜRER » est la 4ème! Donc 4 + 15 + 14 + 1 = 34 ! CQFD...
Albrecht DÜRER était tres fier d‘avoir créé son carré... et il y a avait de quoi l'être!
Albrecht DÜRER
On trouve un autre carré magique d'ordre 4 (n=4) et de valeur 33, et non plus 34, sur la façade de la passion de la cathédrale de la Sagrada Familia de GAUDI à Barcelone… sous une autre forme, car il ne possède pas le 12 ni le 16 qu'il aurait dû avoir, et a 2 doublons, ce qui fait que la somme de ses chiffres fait alors 33 et non plus 34 !
En effet, le nombre 12 a disparu, il ne possède pas le 16, par contre on trouve 2 fois les nombres 14 et 10, mais curieisement, la somme des chiffres dans les deux diagonales fait également 33... ainsi que la somme en dextrogyre comme en sinistrogyre et la somme des 4 chiffres du milieu, comme le carré de DÜRER !
Et la somme de tous ses nombre vaut 132, mais plus 136.
Pourquoi 33... Ce doit être un clin d'oeil de l'architecte à un autre symbole, à savoir que 33 est appelé un « nombre angélique ».
Le nombre angélique « 33 » est considéré comme un « nombre maître » à savoir qu’il est censé avoir une vibration plus élevée, et cela lui donne une signification spirituelle plus importante que les autres nombres.
En numérologie, les « nombres maîtres » (tout comme 11, 22 et 33) sont considérés comme chargés en énergie spirituelle et ont donc une signification plus profonde.
Le nombre 33 est considéré avoir l’énergie de la compassion, de la bénédiction, de l’inspiration, de l’honnêteté, de la bravoure et du courage ! Il en fallait pour construire une telle cathédrale…
Si un lecteur avait une autre explication, qu'il ait la gentillesse de la partager en commentaire de cet article...

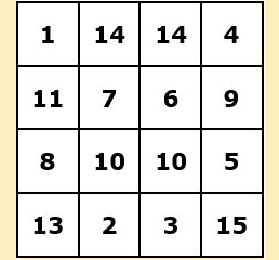
Le carré de GAUDI à l'entrée de sa cathédrale... = 33 !
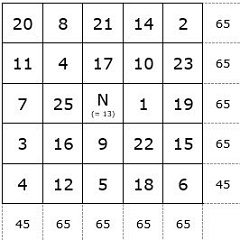
Un carré d'ordre 5, a été sculpté sur un mur de la Place d’Assas à Nîmes, crée en 1989 par le plasticien Martial RAYSSE. Il propose aux visiteurs une expérience philosophique.
Ce carré magique est orné d’un « N » = 13 au centre absent du carré, et en remplaçant 4 par 24 dans l’angle inférieur gauche ; alors toutes les sommes linéaires ont un total de 65 : c’est la constante magique des carrés magiques d’ordre n = 5.
Mais la somme de ses nombres vaut 292.
Un carré d'ordre 5 quelque peu dérangeant : un carré, constitué cette fois avec des lettres et non plus des chiffres, a intrigué les connaisseurs. C'est le carré « SATOR »
On suppose qu’il fut composé approximativement en l’an 79 de notre ère puisqu’il fut découvert dans les ruines de la ville de Pompéi, détruite la même année par l’éruption du Vésuve.
Le carré « SATOR », figure un palindrome* véhiculé par le Christianisme depuis au moins 16 siècles, que l'on retrouve sur plusieurs bâtiments anciens a fait couler beaucoup d’encre.
Fréquemment recopié jusqu’à la Renaissance, ce diagramme possède un riche passé historique que l’on retrouve dans de nombreux pays.
*Un Palindrome est un mot ou une phrase offrant le même sens quand on le lit de gauche à droite ou de droite à gauche. Le carré SATOR est un palindrome continu, où la phrase se déroule indifféremment dans les deux sens :
« SATOR AREPO TENET OPERA ROTAS »
« ROTAS OPERA TENET AREPO SATOR »
La signification pourrait en être : Le sauveur (SATOR: le semeur) sur sa croix (AREPO: la charrue parfois symbole de croix) est maître (TENET) par son sacrifice (OPERA) du destin (ROTAS: les roues donc allusion au destin).
On le trouve aussi sur un mur romain à Oppède dans le Lubéron tout comme dans le palais impérial du Duc de Savoie à Vienne (Autriche).


Carré SATOR d'Oppède (Luberon) et Carré SATOR de Vienne (Autriche)
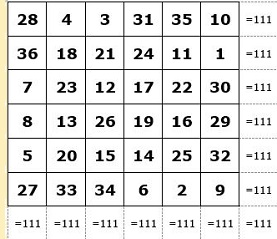
Le carré d'ordre 6 est traditionnellement associé au ciel du Soleil. La somme de tous ses nombres vaut donc 1 + 2 + ... + 36 = 666, et sa valeur est 111.
Ainsi, le fait que 666 est avant tout considéré, notamment par la Kabbale, comme un nombre « solaire », c'est uniquement l'un de ses aspects, négatif (666 : le fameux Nombre du Diable!), qui doit être considéré comme « maléfique », et non le nombre en lui-même, qui garde avant tout cet aspect solaire
Et on retrouve des carrés magiques sur de nombreux autres édifices.
Dans la province de SHAANXI, cette ville chinoise où l'on a découvert la fameuse armée de terre cuite...

l'armée de guerriers de terre cuite (en dimension réelle)